Control Flow Analysis

Control Flow Analysis 정리

1. Control Flow Analysis

컴파일러의 분석에는 두가지로 나누어진다.

• Control flow analysis
  • 제어 흐름을 분석한다.
• Data flow analysis
  • 데이터의 흐름을 분석한다.

이러한 분석을 하는 이유는 코드 최적화 전/후의결과가 서로 identical하기 원하기 때문이다. 즉, 제어 흐름이 바뀌어서도 안되고 데이터의 결과가 달라져서도 안된다. 이 때문에 컴파일러는 CFA, DFA를 진행하고 가능한 최적화를 수행한다.

근데 애초에 최적화를 진행하기 위해서는는 natural loop로 이루어진 코드여야 한다. 다시 말하면, C에서 for와 while문만 사용하고 goto문을 사용하지 않은 코드만 최적화가 된다¹.

이 때문에 컴파일러 최적화에 앞서, 코드가 natural loop로만 이루어졌음을 증명하는것이 아주 중요하다.

결국 이 글의 목적은 코드가 natural loop로만 이루어져 컴파일러가 최적화를 할 수 있는지 보는것이다.

Before start

코드를 line by line으로 분석하는건 말이 안되므로 basic block 개념을 도입한다.

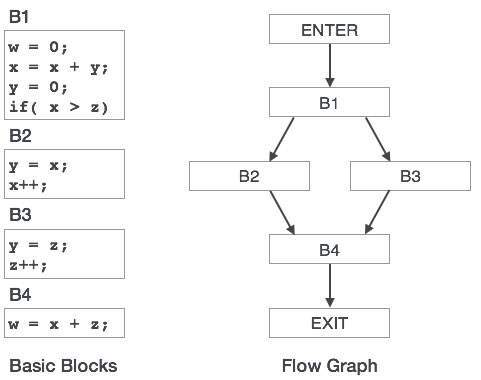
기본 블록 (basic block)은 엔트리 외에는 들어오는 분기가 없고, 출구 외에는 나가는 분기가 없는 직선 코드열이다.

Basicblock from 위키피디아

이에 대한 그림은 아래와 같다.

²

모든 분석 단위는 basicblock이 될 것이다.

2. Natural loop를 어떻게 찾을것인가?

2-1. Dominance Relation(지배 관계)

일반적으로 loop를 생각해보면, for와 while문은 코드 중간부터 시작하는것이 불가능하다. (중간에 끝나는건 가능하다. i.e.)continue,break) 즉, loop 내부 코드들을 접근하려면 loop 시작지점(entry basic block³)을 항상 통과해야 한다. 이를 그래프 이론으로 표현한것이 dominance(지배)라는 개념이다.

4

즉, 위와 같이 entry basic block(B2)은 loop 내부의 모든 basic block들(B2, B3, B4, B5)을 dominate한다. 즉, A block이 B block을 지배한다면

A dominates B or A doms B

라 표시한다. 그리고 B를 A,B,C,D block이 지배할 때, 지배하는 모든 dominator를 나타내는 수학적 기호는

$$dom(B)={ A, B, C, D }$$

이다. 위 그림의 경우 $dom(B5)={ B1, B2, B3, B5 }$이다.

근데 위 그림에서 B1 doms B2지만 loop는 아니다. 그러므로 이 관계는 loop의 일부조건일 뿐임을 알 수 있다.

Dominance Relation의 상속

Dominance relation은 재미있는 수학적 관계를 갖는다. 즉, A가 B를 지배하고 B가 C를 지배하면 A는 C를 지배한다는것이다.(A가 대빵, B가 중간보스, C가 쫄이다.) 즉

A doms B && B doms c == A doms C

이 성질은 하위 블럭에 대한 dominance를 계산하는데 도움을 준다.

2-2. Back edge

Dominance relation이 loop의 조건으로 부족한 이유는 loop의 핵심인 entry point로 복귀하는것이 없기 때문이다.

위 그림에서 ${B1, B2}$ 관계와 다르게 B5는 entry basic block인 B2으로 갈 수 있다(!!). 이 때, 역으로 올라가는 edge를 back edge라 한다. 결국 loop를 구성하기 위해서는 back edge가 존재해야 함을 알 수 있다.

결론적으로 두 basic block $B_x$과 $B_y$에 대해서 아래와 같은 성질을 만족하면 natural loop가 있음을 알 수 있다.

• $B_x$ dominates $B_y$
• $B_y$ has back edges to $B_x$

3. Reducibility

Reducibility는 control flow graph⁵의 특성이다. 이 특성이 중요한 이유는 control flow graph가 모두 natural loop로만 이루어져 있다면 reducible하기 때문이다. 즉, reducible한 코드는 컴파일러가 분석 가능한 코드라는 의미이다.

위의 그림은 control flow graph가 T1-T2 analysis를 통하여 single vertex로 reduce되는 과정을 보여준다. 이러한 방법을 통해 컴파일러는 코드가 분석 가능 여부를 알 수 있다.

T1-T2 analysis

이 analysis의 목적은 reducibility를 체크하기 위함이다. T1-T2 analysis는 크게 2가지 graph transformation으로 이루어져 있다.

T1 transformation

self-loop가 있으면 self-loop를 없앤다.

T2 transformation

Block A에 대하여 유일한 선행 block B이 있다면 A를 B로 합친다.

선행 블럭, 후행 블럭은 entry basic block부터 그래프를 DFS(Depth-first-search)로 진행했을 때의 순서로써 결정된다.

위 T1 transformation과 T2 transformation을 이용하여 graph의 vertex들을 하나로 합칠 수 있다면 graph에서 나타내는 코드는 reducible하다. 아래 예제는 전에 제시했던 reducible한 예와 다르게 irreducible한 예이다.

이 때, T1 transformation은 self-loop이 없으므로 불가능하고, C와 B는 선행블럭이 각각 2개씩 있으므로 T2 transformation도 불가능하다. 그러므로 irreducible하다. 

Node splitting

여기서는 간략하게 언급만 하고 넘어간다. Irreducible 코드인 경우, 노드를 나누어 reducible 코드로 만들 수 있다. 예제는 아래와 같다.

단, $w = w_1 = w_2$이다.

이 방법은 natural loop가 아닌 loop(multi entry loop)을 natural loop로 변환시켜 reducible하게 만든다.

---

1. goto문을 넣게 되면 최적화 문제가 NP hard가 되어서 컴파일 시간이 무지막지하게 늘어난다. 그러기에 goto문이 있으면 컴파일러가 최적화를 포기한다. ↩

2. https://www.tutorialspoint.com/compiler_design/compiler_design_code_optimization.htm ↩

3. https://ko.wikipedia.org/wiki/%EA%B8%B0%EB%B3%B8_%EB%B8%94%EB%A1%9D ↩

4. http://ag-kastens.uni-paderborn.de/lehre/material/compii/aufgaben/blatt2/Loesung2.html ↩

5. 이제까지 다루었던 basic block으로 이루어진 graph이다. ↩